Assessing Phylogenetic Reliability Using RevBayes and $P^{3}$

Overview

This tutorial presents the general principles of assessing the reliability of a phylogenetic inference through the use of posterior predictive simulation (PPS). PPS works by assessing the fit of an evolutionary model to a given dataset, and analyzing several test statistics using a traditional goodness-of-fit framework to help explain where a model may be the most inadequate.

Introduction

Assessing the fit of an evolutionary model to the data is critical as using a model with poor fit can lead to spurious conclusions. However, a critical evaluation of absolute model fit is rare in evolutionary studies. Posterior prediction is a Bayesian approach to assess the fit of a model to a given dataset (Bollback 2002; Brown 2014; Höhna et al. 2018), that relies on the use of the posterior and the posterior predictive distributions. The posterior distribution is the standard output from Bayeisan phylogenetic inference. The posterior predictive distribution represents a range of possible outcomes given the assumptions of the model. The most common method to generate these possible outcomes, is to sample parameters from the posterior distribution, and use them to simulate new replicate datasets (). If these simulated datasets differ from the empirical dataset in a meaningful way, the model is failing to capture some salient feature of the evolutionary process.

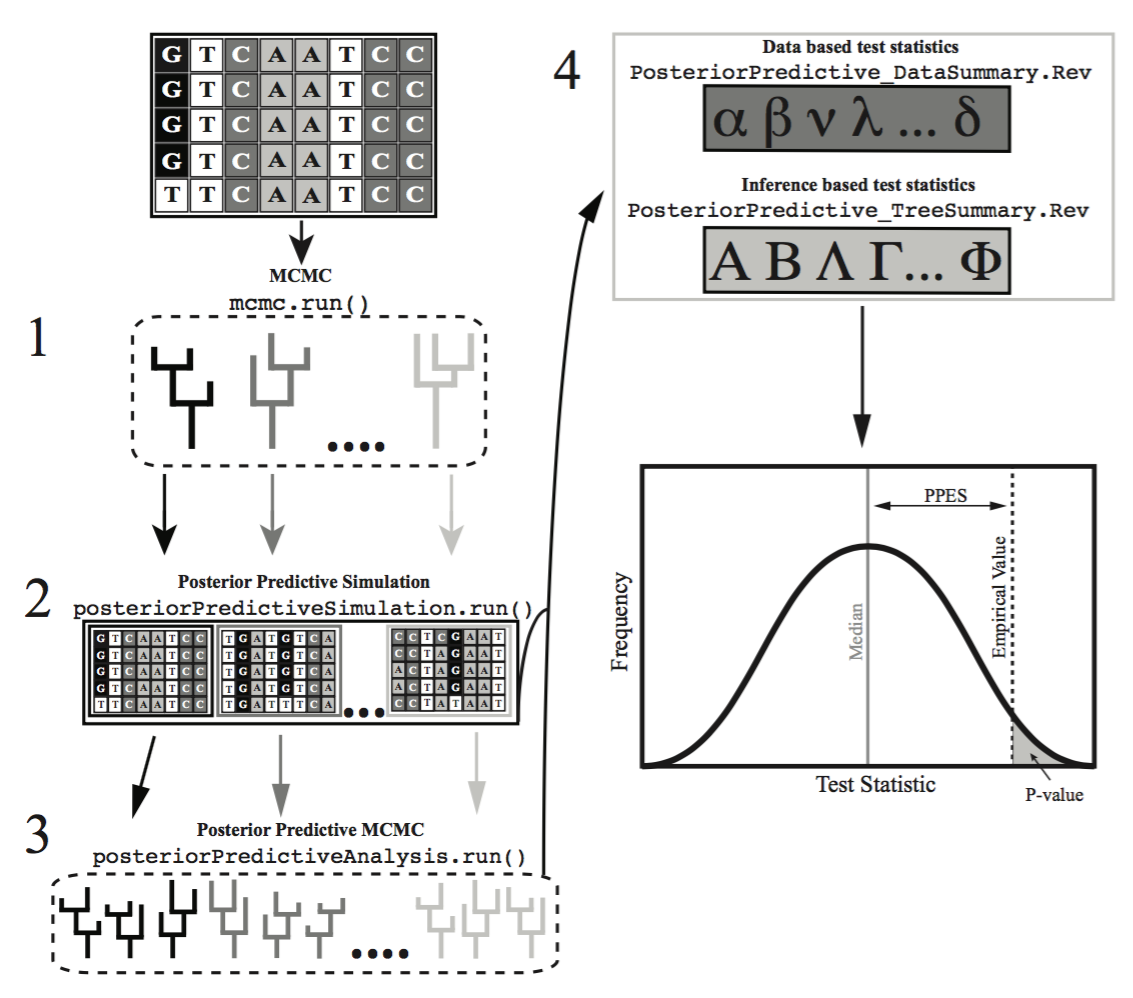
The framework to construct posterior predictive distributions, and compare them to the posterior distribution is conveniently built in to ‘RevBayes‘ (Höhna et al. 2014; Höhna et al. 2016; Höhna et al. 2018). In this tutorial we will walk you through using this functionality to perform a complete posterior predictive simulation on an example dataset.

Data- Versus Inference-Based Comparisons

Most statistics proposed for testing model plausibility compare data-based characteristics of the original data set to the posterior predictive data sets (e.g., variation in GC-content across species). In data-based assessments of model fit one compares the empirical data to data simulated from samples of the posterior distribution. ‘RevBayes‘ additionally implements test statistics that compare the inferences resulting from different data sets (e.g., the distribution of posterior probability across topologies). These are called inference-based assessments of model fit. For these assessments one must run an MCMC analysis on each simulated data set, and then compare the inferences made from the simulated data to the inference made from the empirical data.

In this tutorial we will only cover the data-based method of assessing model plausibility. The inference-based method can be a powerful tool that you may want to explore at another time.

Substitution Models

The models we use here are equivalent to the models described in the previous exercise on substitution models (continuous time Markov models). To specify the model please consult the previous exercise. Specifically, you will need to specify the following substitution models:

• Jukes-Cantor (JC) substitution model (missing reference)
• General-Time-Reversible (GTR) substitution model (missing reference)
• Gamma (+G) model for among-site rate variation (missing reference)
• Invariable-sites (+I) model (missing reference)

Assessing Model Fit with Posterior Prediction

The entire process of posterior prediction can be executed by using the pps_analysis_JC.Rev script in the scripts folder. If you were to type the following command into ‘RevBayes‘:

    source("scripts/pps_analysis_JC.Rev")

the entire data-based posterior prediction process would run on the example dataset. However, in this tutorial, we will walk through each step of this process on an example dataset to explain what is happening in detail.

Empirical MCMC Analysis

To begin, we first need to generate a posterior distribution from which to sample for simulation. This is the normal, and often only, step conducted in phylogenetic studies. Here we will specify our dataset, evolutionary model, and run a traditional MCMC analysis.

This code is all in the data_pp_analysis_JC.Rev file.

Set up the workspace

First, let’s set up some workspace variables we’ll need. We’ll specify a general name to apply to your analysis. This will be used for future output files, so make sure it’s something clear and easy to understand.

    analysis_name = "pps_example"
    model_name = "JC"
    model_file_name = "scripts/pps_"+model_name+"_Model.Rev"

Now specify and read in the input file. This is your sequence alignment in NEXUS format.

    inFile = "data/primates_and_galeopterus_cytb.nex"
    data <- readDiscreteCharacterData(inFile)

Specify the model

Now we’ll call a separate script pps_JC_Model.Rev that specifies the JC model:

    source( model_file_name ) 

If we open the pps_JC_Model.Rev script, most of this script should look familiar from the Nucleotide substitution models. Nevertheless, we will look at some parts of script for a very brief repitition.

    Q <- fnJC(4)

Here we are specifying that we should use the Jukes-Cantor model, and have it applied uniformly to all sites in the dataset. While this obviously is not likely to be a good fitting model for most datasets, we are using it for simplicity of illustrating the process.

    topology ~ dnUniformTopology(names)

This sets a uniform prior on the tree topology.

    br_lens[i] ~ dnExponential(10.0)

This sets an exponential distribution as the branch length prior.

    phylogeny := treeAssembly(topology, br_lens)

This builds the tree by combining the topology with branch length support values.

Run the MCMC

Now let’s run MCMC on our empirical dataset, just like a normal phylogenetic analysis. Here we use the Jukes-Cantor substition model.

    source("scripts/pps_MCMC_Simulation.Rev")

After specifying a model, we will conduct the MCMC analysis with the script pps_MCMC_Simulation.Rev. Much of that script should look familiar from the Nucleotide substitution models, but let’s take a look at the script and break down and revisit some of the major pieces as a refresher. Much of this will be a familiar to you from the Nucleotide substitution models.

First we need to specify some monitors.

    mni = 0
    monitors[++mni] = mnModel(filename="output" + n + "/" + analysis_name + "_posterior.log",printgen=10, separator = TAB)
    monitors[++mni] = mnFile(filename="output" + n + "/" + analysis_name + "_posterior.trees",printgen=10, separator = TAB, phylogeny)
    monitors[++mni] = mnScreen(printgen=1000, TL)
    monitors[++mni] = mnStochasticVariable(filename="output" + n + "/" + analysis_name + "_posterior.var",printgen=10)

Here the monitors are just being advanced by the value of mni which is being incremented each generation.

Next, we will call the MCMC function, passing it the model, monitors and moves we specified above to set to build our mymcmc object.

    mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Specify a burnin for this run.

    mymcmc.burnin(generations=2000,tuningInterval=200)

Finally, we will execute the run for a specified number of generations. The number of generations and printed generations is important to consider here for a variety of reasons, in particular for posterior predictive simulation. When we simulate datasets in the next step, we can only simulate 1 dataset per sample in our posterior. So, while the number of posterior samples will almost always be larger than the number of datasets we will want to simulate, it’s something to keep in mind.

Now let’s actually run the MCMC in ‘RevBayes‘.

    mymcmc.run(generations=10000)

MCMC output

After the process completes, the results can be found in the output_JC folder. You should see a number of familiar looking files, all with the name we provided under the analysis_name variable, pps_example in this case. Since we set the number of runs (nruns=2) in our MCMC, there will be two files of each type (.log .trees .var) with an _N where N is the run number. You will also see 3 files without any number in their name. These are the combined files of the output. These will be the files we use for the rest of the process. If you open up one of the combined .var file, you should see that there are 1000 samples. This was produced by our number of generations (10,000) divided by our number of printed generations (10), which we specified earlier. This is important to note, as we will need to thin these samples appropriately in the next step to get the proper number of simulated datasets.

Posterior Predictive Data Simulation

The next step of posterior predictive simulation is to simulate new datasets by drawing samples and parameters from the posterior distribution generated from the empirical MCMC anlaysis.

In the pps_analysis_JC.Rev script, that is conducted using the following lines of RevScript:

    source("scripts/pps_Simulation.Rev")

Let’s take a look at each of the calls in the pps_Simulation.Rev script so that we can understand what is occurring.

First, we read in the trace file of the Posterior Distribution of Variables.

    trace = readStochasticVariableTrace("output_" + model_name + "/" + analysis_name + "_posterior.var", delimiter=TAB)

Now we call the posteriorPredictiveSimulation() function, which accepts any valid model of sequence evolution, and output directory, and a trace. For each line in the trace, it will simulate a new dataset under the specified model.

    pps = posteriorPredictiveSimulation(mymodel, directory="output" + "/" + analysis_name + "_post_sims", trace)

Now we run the posterior predictive simulation, generating a new dataset for each line in the trace file that was read in. This is the part where we need to decide how many simulated datasets we want to generate. If we just use the pps.run() command, one dataset will be generated for each sample in our posterior distribution. In this case, since we are reading in the combined posterior trace file with 2000 samples, it would generate 2000 simulated datasets. If you want to generate fewer, say 1000 datasets, you need to use the thinning argument as above. In this case, we are thinning the output by 2, that is we are dividing our number of samples by 2. So that in our example case, we will end up simulating 1000 new datasets.

    pps.run(thinning=2)

This process should finish in just a minute or two. If you look in the output_JC folder, there should be another folder called pps_example_post_sims. This folder is where the simulated datasets are saved. If you open it up, you should see 100 folders named posterior_predictive_sim_N. Where N is the number of the simulated dataset. In each of these folders, you should find a seq.nex file. If you open one of those files, you’ll see it’s just a basic NEXUS file. These will be the datasets we analyze in the next step.

Calculating the Test Statistics

Now we will calculate the test statistics from the empirical data and the simulated data sets. The part in the pps_analysis_JC.Rev script that generates the test statistics is the following line:

    num_post_sims = listFiles(path="output_"+model_name+"/" + analysis_name + "_post_sims").size()
    source("scripts/pps_DataSummary.Rev")

We will look at the major concepts of the pps_DataSummary.Rev to better understand how it works. For a more complete discussion of the statistics involved, please review (Höhna et al. 2018). In general, this script and these statistics work by calculating the statistics of interest across each posterior distribution from the simulated datasets, and comparing those values to the values from the empirical posterior distribution.

The current version of this script generates over 30 summary statistics including:

• Number Invariant Sites
• Max Pairwise Difference
• Max GC Content
• Min GC Content
• Mean GC Content

There are functions built-in to ‘RevBayes‘ to calculate these values for you. Here are some examples from the pps_DataSummary.Rev script:

    max_pd          = sim_data.maxPairwiseDifference( excludeAmbiguous=FALSE )
    mean_gc_1       = sim_data.meanGcContentByCodonPosition(1, excludeAmbiguous=FALSE )
    var_gc_1        = sim_data.varGcContentByCodonPosition(1, excludeAmbiguous=FALSE )

These same statistics are calculated for both the posterior distributions from the simulated datasets and the posterior distribution from the empirical dataset.

Calculating P-values and effect sizes

Once we have the test statistics calculated for the simulated and empirical posterior distributions, we can compare the simulated to the empirical to get a goodness-of-fit. One simple way to do this is to calculate a posterior predictive Pvalue for each of the test statistics of interest. This is done in the data_pp_analysis_JC.Rev with the following lines :

    emp_pps_file = "results_" + model_name + "/empirical_data_" + analysis_name + ".csv"
    sim_pps_file = "results_" + model_name + "/simulated_data_" + analysis_name + ".csv"
    outfileName = "results_" + model_name + "/data_pvalues_effectsizes_" + analysis_name + ".csv"
    source("scripts/pps_PValues.Rev")

The 4 posterior predictive P-values currently calculated by ‘RevBayes‘ are:

• Lower 1-tailed
• Upper 1-tailed
• 2-tailed
• Midpoint

The posterior predictive P-value for a lower one-tailed test is the proportion of samples in the distribution where the value is less than or equal to the observed value, calculated as:

The posterior predictive P-value for a lower one-tailed test is the proportion of samples in the distribution where the value is greater than or equal to the observed value, calculated as:

and the two-tailed posterior predictive P-value is simply twice the minimum of the corresponding one-tailed tests calculated as:

Finally, the midpoint posterior predictive P-value iscalculated as:

For more a more detailed description please look at (Höhna et al. 2018).

The pps_PValues.Rev script

Let’s take a look at the pps_PValues.Rev script to get a better idea of what is happening.

Using the equations outlined above, this script reads in the simulated and empirical data we just calculated, and calls a few simple functions for each of the test statistics:

    ## Calculate and return a vector of lower, equal, and upper pvalues for a given test statistic
    p_values <- posteriorPredictiveProbability(numbers, empValue)

    ## 1-tailed
    lower_p_value <- p_values[1] 
    equal_p_value <- p_values[2] 
    upper_p_value <- p_values[3] 

    ## mid-point
    midpoint_p_value = lower_p_value + 0.5*equal_p_value

    ## 2-tailed
    two_tail_p_value = 2 * (min(v(lower_p_value, upper_p_value)))

these snippets calculate the various p-values of interest to serve as our goodness-of-fit test.

Posterior predictive effect size

Another way that you can calculate the magnitude of the discrepancy between the empirical and PP datasets is by calculating the effect size of each test statistic. Effect sizes are useful in quantifying the magnitude of the difference between the empirical value and the distribution of posterior predictive values. The test statistic effect size can be calculated by taking the absolute value of the difference between the median posterior predictive value and the empirical value divided by the standard deviation of the posterior predictive distribution (missing reference). Effect sizes are calculated automatically for the inference based test statistics in the P analysis. The effect sizes for each test statistics are stored in the same output file as the P-values.

    effect_size = abs((m - empValue) / stdev(numbers))

calculates the effect size of a given test statistic.

Viewing the Results

Once execution of the script is complete, you should see a new directory, named results_JC. In this folder there should be 3 files. Each of these is a simple comma-delimited (csv) file containing the test statistic calculation output.

• empirical_pps_example.csv
• pps_example.csv
• pvalues_pps_example.csv

If you have these 3 files, and there are results in them, you can go ahead and quit ‘RevBayes‘.

    q()

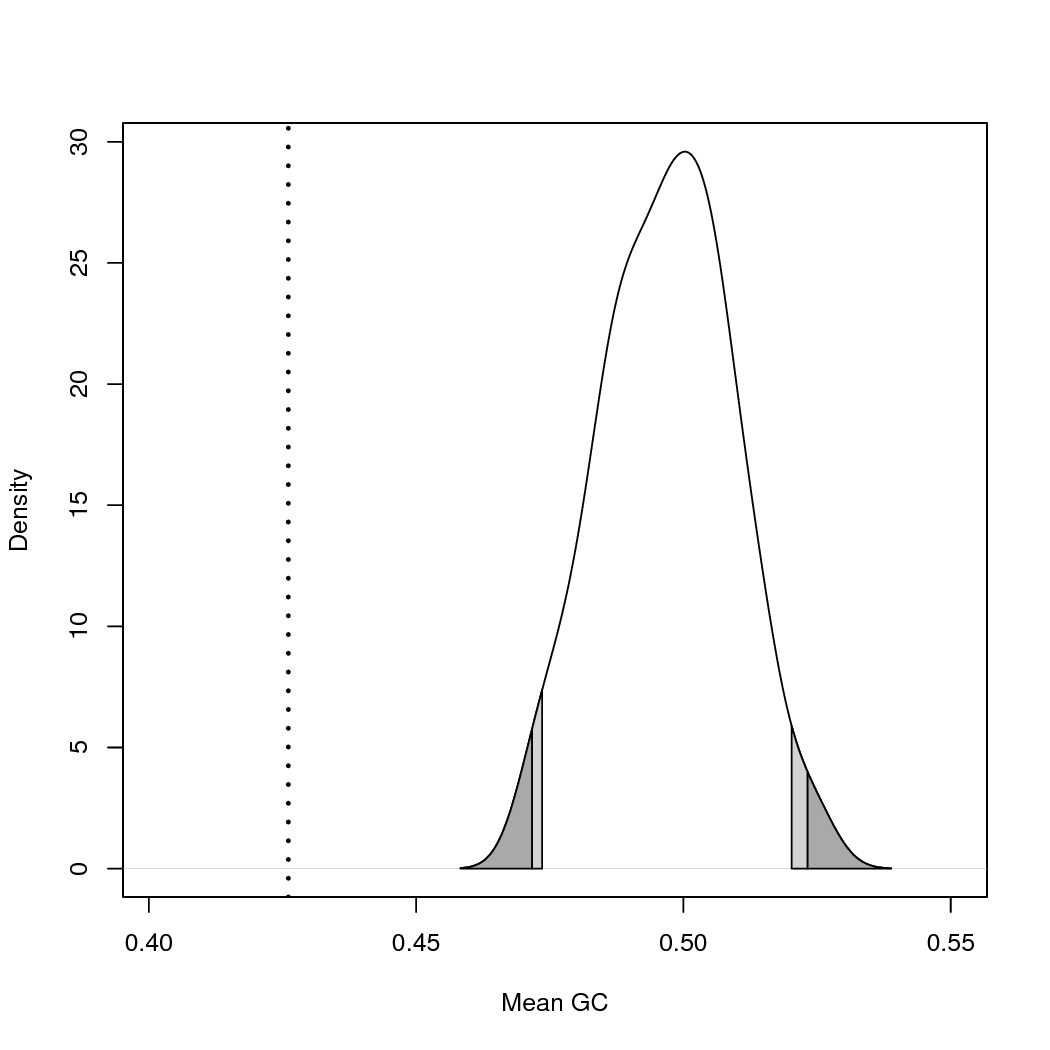
You can get an estimate of how the model performed by examining the P-values in the data_pvalues_effectsizes_pps_example.csv file. In this example, a quick view shows us that most of the statistics show a value less than 0.05. This leads to a rejection of the model, suggesting that the model employed is not a good fit for the data. This is the result we expected given we chose a very simplistic model (JC) that would likely be a poor fit for our data. However, it’s a good example of the sensitivity of this method, showing how relatively short runtimes and a low number of generations will still detect poor fit.

You can also use Rto plot the results. Run the Rscript scripts/plot_results.R. This will generate a pdf plot for every test statistic. See and its legend to learn how to interpret these plots.

Exercises

Included in the scripts folder is a second model script called pps_GTR_Model.Rev. As a personal exercise and a good test case, take some time now, and run the same analysis, substituting the pps_GTR_Model.Rev model script for the pps_JC_Model.Rev script we used in the earlier example. You should get different results, this is an excellent chance to explore the results and think about what they suggest about the fit of the specified model to the dataset.

Additional Exercises

Some Questions to Keep in Mind:

• Do you find the goodness-of-fit results to suggest that the GTR or JC model is a better fit for our data?

• Which test statistics seem to show the strongest effect from the use of a poorly fitting model?

Batch Processing of Large Datasets

In this tutorial you have learned how to use ‘RevBayes‘ to assess the fit of a substitution model to a given sequence alignment. As you have discovered, the observed data should be plausible under the posterior predictive simulation if the model is reasonable. In phylogenetic analyses we choose a model, which explicitly assumes that it provides an reasonable explanation of the evolutionary process that generated our data. However, just because a model may be the ’best’ model available, does not mean it is an appropriate model for the data. This distinction becomes both more critical and less obvious in modern analyses, where the number of genes often number in the thousands. Posterior predictive simulation in ‘RevBayes‘, allows you to easily check model fit for a large number of genes by using global summaries to check the posterior predictive distributions with a comfortable goodness-of-fit style framework.

The process described above is for a single gene or alignment. However, batch processing a large number of genes with this method is a relatively straight forward process.

‘RevBayes‘ has built in support for MPI so running ‘RevBayes‘ on more than a single processor, or on a cluster is as easy as calling it with openmpi.

For example:

    mpirun -np 16 rb-mpi scripts/full_analysis.Rev

would run the entire posterior predictive simulation analysis on a single dataset using 16 processors instead of a single processor. Use of the MPI version of ‘RevBayes‘ will speed up the process dramatically.

Setting up the full_analysis.Rev script to cycle through a large number of alignments is relatively simple as well. One easy way is to provide a list of the data file names, and to loop through them. As an example:

    data_file_list = "data_file_list.txt" 
    data_file_list <- readDiscreteCharacterData(data_file_list)
    file_count = 0

    for (n in 1:data_file_list.size()) {

    FULL_ANALYSIS SCRIPT GOES HERE

    file_count = file_count + 1
    }

Then, anywhere in the full analysis portion of the script that the lines

    inFile = "data/8taxa_500chars_GTR.nex"
    analysis_name = "pps_example"

appear, you would replace them with something along the lines of:

    inFile = n
    analysis_name = "pps_example_" + file_count

This should loop through all of the data files in the list provided, and run the full posterior predictive simulation analysis on each file. Using a method like this, and combining it with the MPI call above, you can scale this process up to multiple genes and spread the computational time across several cores to speed it up.

1. Bollback J.P. 2002. Bayesian model adequacy and choice in phylogenetics. Molecular Biology and Evolution. 19:1171–1180. 10.1093/oxfordjournals.molbev.a004175
2. Brown J.M. 2014. Predictive approaches to assessing the fit of evolutionary models. Systematic Biology. 63:289–292. 10.1093/sysbio/syu009
3. Höhna S., Landis M.J., Heath T.A., Boussau B., Lartillot N., Moore B.R., Huelsenbeck J.P., Ronquist F. 2016. RevBayes: Bayesian Phylogenetic Inference Using Graphical Models and an Interactive Model-Specification Language. Systematic Biology. 65:726–736. 10.1093/sysbio/syw021
4. Höhna S., Coghill L.M., Mount G.G., Thomson R.C., Brown J.M. 2018. P^3: Phylogenetic Posterior Prediction in RevBayes. Molecular Biology and Evolution. 35:1028–1034. 10.1093/molbev/msx286
5. Höhna S., Heath T.A., Boussau B., Landis M.J., Ronquist F., Huelsenbeck J.P. 2014. Probabilistic Graphical Model Representation in Phylogenetics. Systematic Biology. 63:753–771. 10.1093/sysbio/syu039