Convergence assessment

Phylogenetic convergence assessment using the R package Convenience

Luiza Fabreti and Sebastian Höhna

Last modified on May 17, 2021

Overview

Prerequisites

Data files and scripts

Example output

Overview

This tutorial covers convergence assessment of a Bayesian phylogenetic analysis using the R package Convenience.

Convergence of an MCMC analysis is crucial to assure that the chain has sampled from the stationary distribution and that we have sufficiently many samples to approximate the posterior distribution. That is, the MCMC has explored the parameter space long enough to reach the true posterior distribution of the parameters and the values we are sampling belong to that distribution. Theory says that a chain that runs through an infinite time, will reach convergence. For our practical problem, we need to make a decision of when we have sampled enough to take a good estimate of the desired parameters. Here we will show how to test if we have enough samples or not.

An ideal solution would be to analytically calculate the number of steps needed to reach convergence. This, however, has turned out to be unfeasible because the number of samples depends on the specific model, the specific moves applied within the MCMC simulation, and the given dataset.

Since we lack a theoretical convergence assessment, what is broadly done in the MCMC field is analyze the output from the MCMC for lack of convergence. To do so, we have to keep in mind two aspects of an analysis that has reached convergence: precision and reproducibility. Precision means that if we run the chain longer, we do not change the estimates (e.g., the posterior mean estimate). While reproducibility means that if we run another independent chain, we get the same estimates. Precision can be evaluated by checking that we have sufficiently many samples because more samples lead to less variance in the estimates (e.g., the standard error of the mean). Reproducibility, on the other hand, can be evaluated by comparing independent chains run under the same model. Therefore, it’s recommended to run at least two or better four replicates when performing MCMC analyses.

Another best practice is to remove the initial samples from the chain. Those initial iterations are called burn-in. By that we try to get rid of the samples that are not taken from the stationary distribution.

One last concept we need to keep in mind is the Effective Sample Size (ESS), i.e., the number of independent samples generated by our MCMC sampler. The ESS takes into account the correlation between samples within a chain. Low ESS values represent high autocorrelation in the chain. If the autocorrelation is higher, then the uncertainty in our estimates is also higher.

Criteria for Convergence using in Convenience

Now that we learned about convergence, let’s take a look into the criteria in the Convenience package:

The output of a phylogenetic analysis most commonly consists of two types of parameters:

To assess convergence for these parameters, the Convenience package evaluates:

The comparison between windows of the same run works by dividing the full length of the run into 5 windows (subsets) and comparing the third and fifth window. This comparison is used to determine the size of the burn-in. A sufficient burn-in will lead to windows that sampled values from the same distribution. Finding the appropriate burn-in size is done automatically in the Convenience package. The package tests burn-in of 0, 10%, 20%, 30%, 40% and 50%. If the required burn-in is higher than 50% of the length of the MCMC, we recommend re-running the MCMC.
In Figure we can see a trace plot for the tree length from the example provided in this tutorial. The trace plot shows the sampled values over the iterations of the MCMC. The highlighted areas of the figure show the third and fifth window of the run.

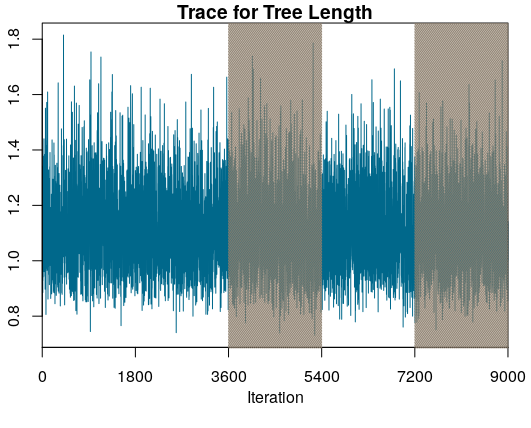
Trace plot of the tree length for our example analysis. The shaded areas show the third and fifth windows of the run.

How do we compare windows and runs?

For the continuous parameters, the comparison is made with the two-sample Kolmogorov-Smirnov (KS) test, a non-parametric statistical test for equality of probability distributions. Two samples will be equal when the KS value is below a given threshold. The KS value (D) is calculated:

\[{D}_{m,n} = \max_{x} |{F_{1,m}(x) - G_{2,n}(x)}|\]

F(x) and G(x) are the empirical distribution functions for the samples with size m and n, respectively. The two samples will be drawn from different distributions, at level $\alpha$, when:

\[{D}_{m,n} > c(\alpha) \sqrt{\frac{m + n}{m\times n}}\]

with

\[c(\alpha) = \sqrt{-\ln({\frac{\alpha}{2})\times \frac{1}{2}}}\]

The phylogenetic tree is evaluated regarding the bipartitions or splits. Therefore, the comparisons are made using the frequency of a given split between intervals of the same run or between different runs.

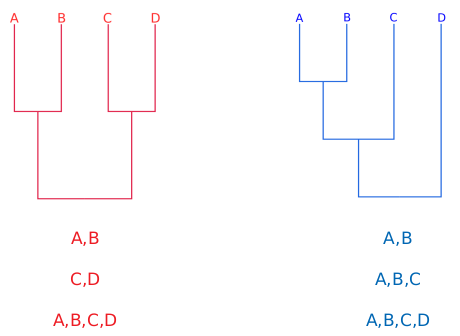
Two example trees with tips A, B, C, D and the splits seen at each tree.

Thresholds

The current state of convergence assessment in Bayesian phylogenetics relies mainly on visual tools (e.g., Tracer) and ESS thresholds that have no clear theory to support them (Rambaut et al. 2018). The motivation for the Convenience package is to provide an easy-to-use framework with clear thresholds for each convergence criterion.

We derive a minimum value for the ESS based on a normal distribution and the standard error of the mean (SEM). How much error in our estimate of the posterior mean should we find acceptable? Clearly, the mean estimate for a distribution with a large variance does not need to be as precise as the mean estimate for a distribution with a small variance. However, relative to the variance/spread of the distribution, what percentage is acceptable? We suggest to use a SEM smaller of 1% of the 95% probability interval of the distribution, which is equivalent to say that the allowed error of the mean is four times the standard deviation of the distribution. (Note that you can derive a different ESS value for any other threshold that you like.) From this SEM, we can derive the ESS with:

\[SEM = \frac{\sigma}{\sqrt{ESS}}\] \[\frac{\sigma}{\sqrt{ESS}} < 1\% \times 4 \times \sigma\] \[ESS > \frac{1}{0.04^2}\] \[ESS > 625\]

An ESS of 625 is therefore the default value for the convenience package.

For the KS test, the threshold is the critical value for $\alpha$ = 0.01 and the sample size is the calculated threshold for the ESS, 625. With these values, the threshold for the KS test is ${D}_{crit}$ = 0.0921.

Split Frequencies

To date, the most often test to assess convergence of split frequencies is the average standard deviation of split frequencies (ASDSF) (Nylander et al. 2008). The frequency of each split is computed for two separate MCMC runs and the difference between the two split frequency estimates is used. The ASDSF is problematic for two reasons: (1) for large trees with many splits that have posterior probabilities close to 0.0 or 1.0 will overwhelm the ASDSF and hence even a single split that is present in all samples in run 1 (thus a posterior probability of 1.0) and is never present in any sample in run 2 (thus a posterior probability of 0.0) might not be detected, and (2) the expected difference in split frequency depends on the true split frequency (see Figure ).

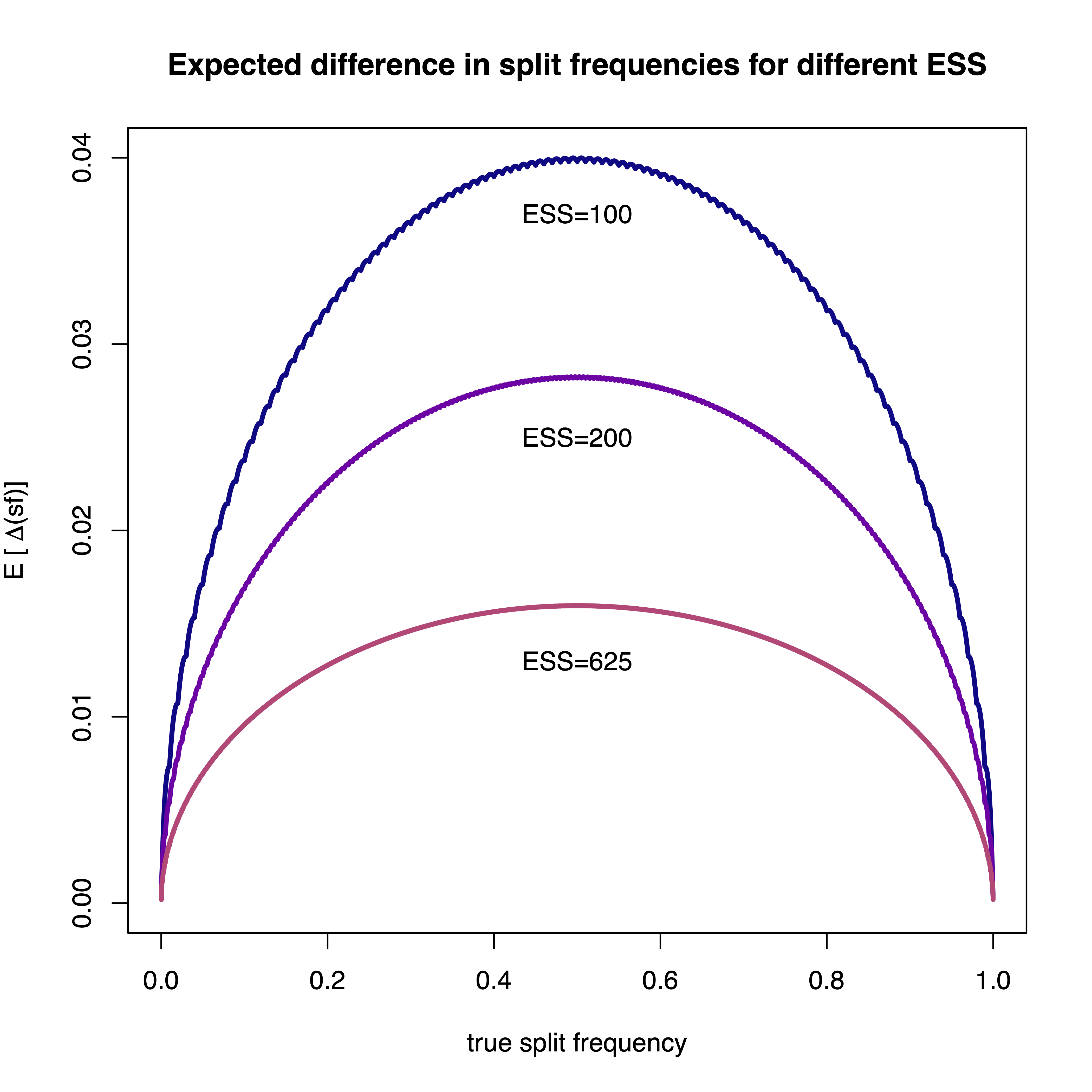
The expected difference in split frequencies for ESS of 100, 200 and 625. The x-axis is the true value of the split frequency. The y-axis is the expected difference in split frequencies. The effect of increasing the ESS is the decrease of differences in frequency of sampled splits.

Instead of the ASDSF we use the ESS of each split. We transform each split into a chain of absence and presence values; if the split was present in the i-th tree then we score the i-th value of the chain as a 1 and 0 otherwise. This sequence of absence and presence observations (0s and 1s) allows us to apply standard methods to compute ESS values and thus we can use the same ESS threshold of 625 as for our continuous parameters.

With the ESS threshold for the splits, we can estimate the expected difference in splits frequencies (EDSF) and use the 95% quantile as a threshold for the split differencies. The expected difference ($ {E}[\Delta^{sf}_{p}] $) between two samples is calculated as the ‘mean absolute difference’, with N as the ESS:

\[{E}[\Delta^{sf}_{p}] = \sum\limits_{i=0}^N \sum\limits_{j=0}^N \left(|\frac{i}{N} - \frac{j}{N}| \times P_{binom}(i|N,p) \times P_{binom}(j|N,p) \right)\]

Summary

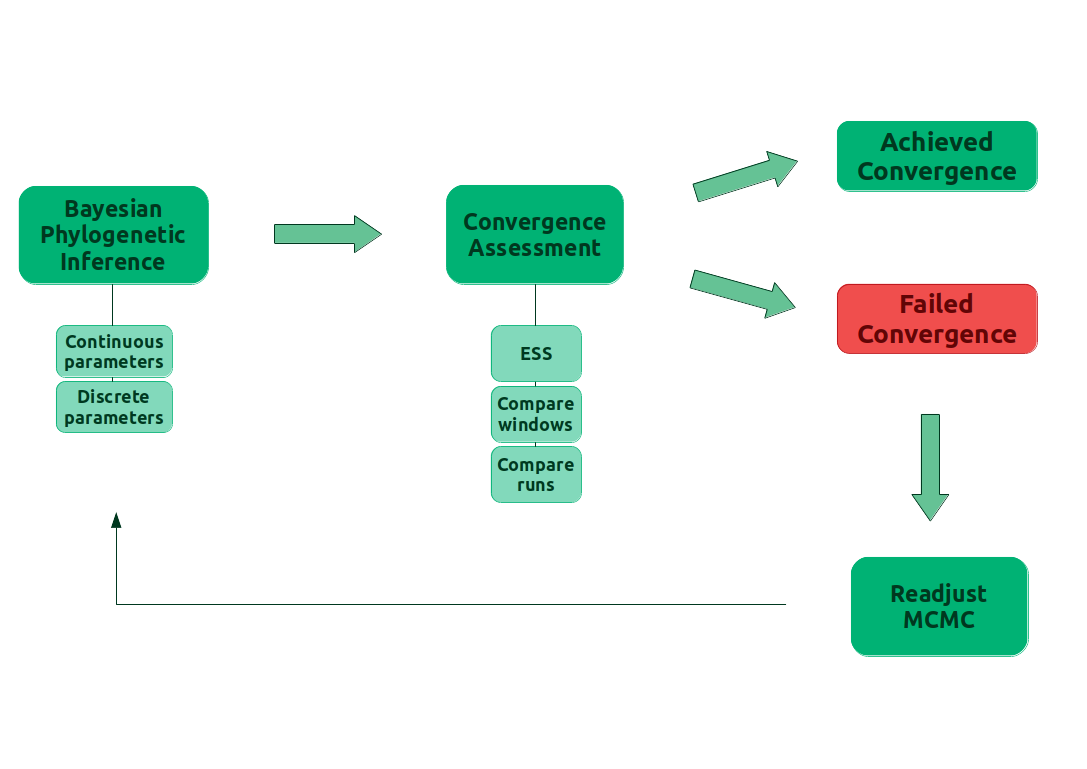
provides an overview of the convergence assessment described before and implemented in the package Convenience.

Overview of the workflow in the convergence assessment.

Convenience

Install

To install Convenience, we need first to install the package devtools. In R, type the commands:

install.packages("devtools")
library(devtools)
install_github("lfabreti/convenience")
library(convenience)

Functions

Here is a list of the functions the package uses to assess convergence:

Example

First, download the files listed as example output files on the top left of this page. Save them in a folder called output. These files are the output from a phylogenetic analysis performed with a dataset from bears. The nucleotide substitution model was GTR+$\Gamma$+I and the MCMC was set to run 2 independent runs. The package also works if your analysis has only one run of the MCMC. But the part to compare runs will not be evaluated. Therefore, it is not possible to say that your MCMC result is reproducible. We strongly advise on running more than 1 run.

Let’s run the checkConvergence function with our example output in a directory (this step may take a few minutes):

check_bears <- checkConvergence("output/")

We can also list the names of the files:

check_bears <- checkConvergence( list_files = c("bears_cytb_GTR_run_1.log", "bears_cytb_GTR_run_1.trees", "bears_cytb_GTR_run_2.log", "bears_cytb_GTR_run_2.trees") )

To better understand what checkConvergence is doing, take a look at . The first step consists of the user setting up the precision in the standard error of the mean for our estimates. The thresholds for ESS, KS test and difference in split frequencies will be calculated based on the precision. Then the function reads in the MCMC output, from the files provided by the user, and computes the quantities used in the criteria for convergence. Afterwards, the function checks if the computed quantities are within the calculated thresholds. Finally, the function reports wheter the MCMC has converged or not, the computed quantities and, in case of non convergence, the parameters that failed to achieve the desired thresholds.

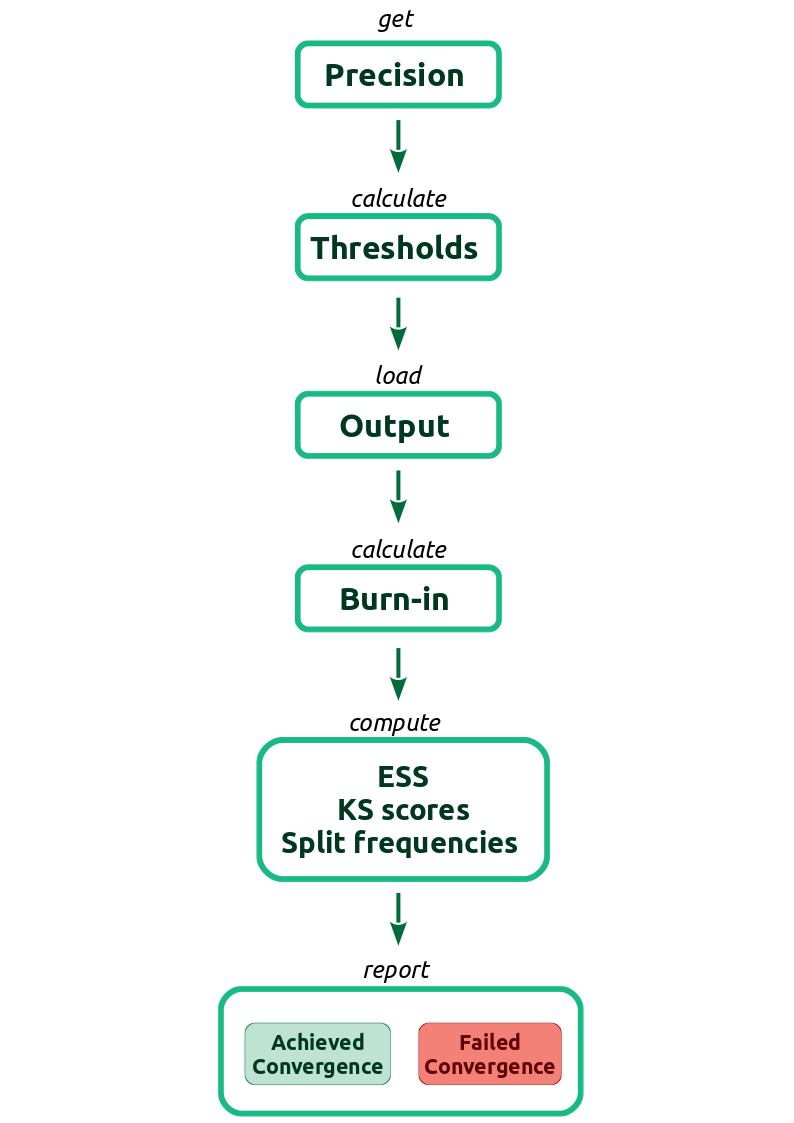
Summary of the process in the checkConvergence function. SF is the abbreviation for split frequencies.

Now, let’s see the output from checkConvergence by typing check_bears. The output message includes:

To check the calculated parameters for the continuous parameters type:
Means: output$continuous_parameters$means
ESS: output$continuous_parameters$ess
KS score: output$continuous_parameters$compare_runs

To check the calculated parameters for the splits type:
Frequencies of splits: output$tree_parameters$frequencies
ESS: output$tree_parameters$ess
Difference in frequencies: output$tree_parameters$compare_runs

To check the full summary message with splits and parameters excluded from the analysis type:
output$message_complete

We can see that check_bears has 4 elements: message, message_complete, converged, continuous_parameters and tree_parameters.

  1. message: a summary of the convergence assessment;
  2. message_complete: the summary from message plus: (1) the splits excluded from the assessment for having frequency above 0.975 or below 0.025 (when applicable), (2) the continuous parameters excluded from the assessment for having no variation during the MCMC (when applicable);
  3. converged: a boolean that has TRUE if the analysis converged and FALSE if it did not converge;
  4. continuous_parameters: a list with means, ESS and KS-scores between runs;
  5. tree_parameters: a list with frequencies, ESS and split frequencies between runs.

In case the analysis has failed to converge, another element will be on the output list: failed with the parameters that failed the criteria for convergence.

We can generate tables with general information for the continuous parameters the splits with the commands:

printTableContinuous(check_bears)

  means ESS
alpha 1.603954589 8921.945
er.1. 0.015576521 10705.048
er.2. 0.505904352 11570.794
er.3. 0.006423004 5683.824
er.4. 0.009572443 18078.730
er.5. 0.454927376 15992.299
er.6. 0.007596305 4368.023
p_inv 0.532339279 3306.411
pi.1. 0.293497210 10057.477
pi.2. 0.301726522 11016.263
pi.3. 0.135420687 9775.079
pi.4. 0.269355587 9885.677
sr.1. 0.216077996 10275.761
sr.2. 0.550663747 16053.336
sr.3. 1.015625752 11775.210
sr.4. 2.217632528 3842.496
TL 1.112491969 7677.455

printTableSplits(check_bears)

  frequencies ESS
Helarctos_malayanus Ursus_americanus 0.09 17127.93
Melursus_ursinus Ursus_arctos Ursus_maritimus 0.18 18074.54
Helarctos_malayanus Melursus_ursinus Ursus_americanus Ursus_thibetanus 0.32 15526.14
Helarctos_malayanus Ursus_americanus Ursus_arctos Ursus_maritimus Ursus_thibetanus 0.50 15731.22
Ursus_americanus Ursus_thibetanus 0.89 15269.03

Convenience also provides plot functions to facilitate showing that convergence has been achieved. The functions plotEssContinuous and plotEssSplits plot the histogram of the ESS values for the continuous parameters and the splits, respectively. The function plotKS plots a histogram of the KS values for the continuous parameters. And the function plotDiffSplits yields a plot for the calculated difference in splits frequency.

The plots generated with Convenience for summarizing and visualizing the results from the convergence assessment. The top-left figure shows the histogram of calculated ESS values for the model parameters (continuous parameters). The bottom-left figure shows the histogram of calculated ESS for the splits. In both histograms the grey dotted lines represents the threshold of 625. The bottom-right plot is the histogram of the Kolmogorov-Smirnov (KS) for the model parameters, the dotted grey line represents the threshold for the KS test. The bottom-left figure shows the observed difference is split frequencies in the green dots and the expected difference between split frequencies (EDSF) in the grey curve. For all plots, the grey area shows where the parameters should be for convergence to be achieved.

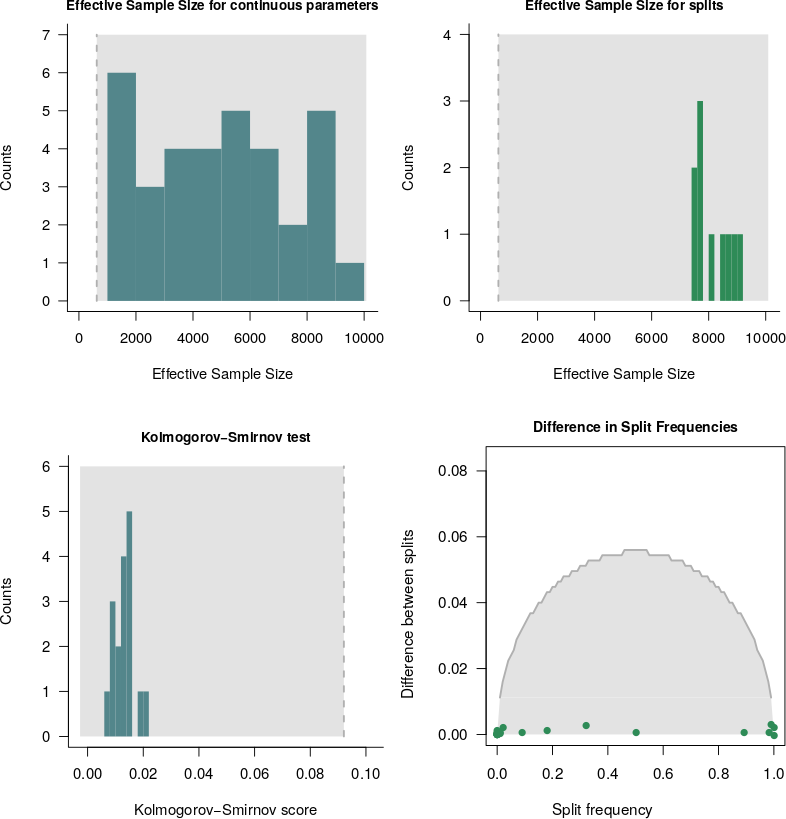
We can see that, for all figures, all continuous parameters and splits have an ESS above the threshold. This is what we would have expected for a MCMC that has converged. The KS histogram shows that all KS values calculated for the continuous parameters are below the threshold. This means that the parameters are drawn from the same distribution for both runs of our analysis. Therefore, if convergence is achieved for a given analysis, the histogram for the KS values should be similiar to this plot. The calculated differences in split frequencies fall below the threshold curve in grey. When convergence is not achieved, some dots would be above the threshold curve.

It is also possible to plot the histogram of the KS values for the comparisons one-on-one when the MCMC analysis have more than 2 runs. The function for this plot is plotKS.pooled. The following figure is an example of this plot.

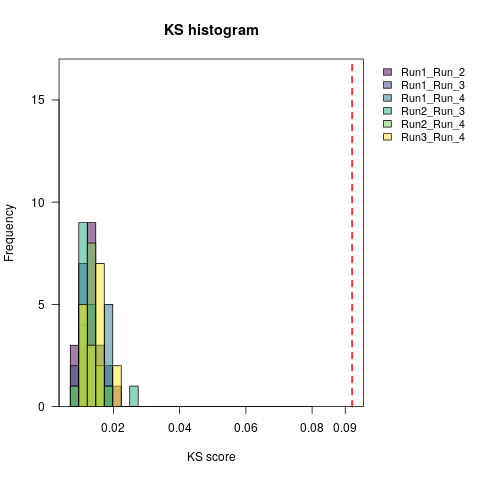
Histogram of the calculated KS values for the one-on-one comparison between runs. Each color represents a different comparison of runs, as shown in the legend. The x-axis is the KS values and the y-axis is the frequency. The red dotted line represents the threshold for the KS score.

In this example, we observe again that all KS values are below the threshold. Which means that, for this criterion, convergence has been achieved. Now that we learned how to use the package and how to interpret the results, let’s practice with some exercises.

Exercise 1

Check for convergence in the output generated in the Nucleotide Substitution Models tutorial.

Which analysis have converged?

Convergence failure

You can see that the output is different when we have a failure in convergence. We have more information in the text output and 2 extra elements failed and failed_names. The element failed has a summary text of what failed in our analysis. The element failed_names has the specifics about the parameters that failed, like the name of the parameter or the split and if it failed in checking for the ESS, the comparison between windows or between runs.

shows the failed message for the convergence assessment on the analysis from Exercise 1 with the GTR+$\Gamma$+I nucleotide substitution model.

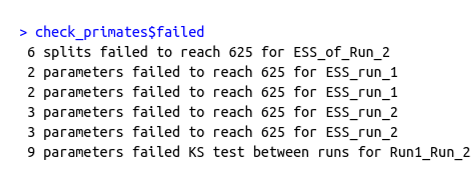
The output from the command check_primates$failed showing a summary of the number of parameters that have failed a certain criterion.

Exercise 2

Exercise 3

In this case we should check only the continuous parameters (log files). Because the trees sampled throughout the MCMC have different number of tips due to the fossil record.

What to do

When we face a convergence failure, there are a few options of what to do in our MCMC to overcome this problem. The suggestions here come from experience, rather than theoretical proofs. We can divide our MCMC that lack convergence by the number of parameters that failed:

For the first case, we should adjust the MCMC to be more efficient. This can be done by increasing the weights on the moves of the parameters that failed, using other MCMC algorithms (such as adaptive MCMC or Metropolis-Coupled MCMC), increasing the number of iterations, etc. In the second case, we should increase the weights on the moves or even add more moves for the specific parameters that failed.

  1. Nylander J.A.A., Wilgenbusch J.C., Warren D.L., Swofford D.L. 2008. AWTY (are we there yet?): a system for graphical exploration of MCMC convergence in Bayesian phylogenetics. Bioinformatics. 24:581.
  2. Rambaut A., Drummond A.J., Xie D., Baele G., Suchard M.A. 2018. Posterior Summarization in Bayesian Phylogenetics Using Tracer 1.7. Systematic Biology. 67:901–904. 10.1093/sysbio/syy032
  3. Warren D.L., Geneva A., Swofford D.L., Lanfear R. 2016. rwty: R We There Yet. A package for visualizing MCMC convergence in phylogenetics.