Introduction to Posterior Prediction

Overview

This tutorial introduces the basic principles of posterior predictive model checking. The goal of posterior prediction is to assess the fit between a model and data by answering the following question: Could the model we’ve assumed plausibly have produced the data we observed?

To perform posterior prediction, we simulate datasets using parameter values drawn from a posterior distribution. We then quantify some characteristic of both the simulated and empirical datasets using a test statistic (or a suite of test statistics), and we ask if the value of the test statistic calculated for the empirical data is a reasonable draw from the set of values calculated for the simulated data. If the empirical test statistic value is very different from the simulated ones, our model is not doing a good job of replicating some aspect of the process that generated our data.

At the end of this tutorial, you should understand the goal of posterior predictive model checking and the steps involved to carry it out in RevBayes.

Introduction

A good statistical model captures important features of observed data using relatively simple mathematical principles. However, a model that fails to capture some important feature of the data can mislead us. Therefore, it is important to not only compare the relative performance of models (i.e., model selection), but also to test the absolute fit of the best model (Bollback 2002; Brown 2014; Brown 2014; Höhna et al. 2018; Brown and Thomson 2018). If the best available model could not have plausibly produced our observed data, we should be cautious in interpreting conclusions based on that model.

Posterior prediction is a technique to assess the absolute fit of a model in a Bayesian framework (Bollback 2002; Brown and Thomson 2018). Posterior prediction relies on comparing the observed data to data simulated from the model. If the simulated data are similar to the observed, the model could reasonably have produced our observations. However, if the simulated data consistently differ from the observed, the model is not capturing some feature of the data-generating process.

An Example

To illustrate the steps involved in posterior prediction, we’ll begin with a non-phylogenetic example. Here, we will examine a hypothetical dataset of trait values sampled from a sexually dimorphic population. However, for the purposes of our tutorial, we will say that we do not yet realize that sexual dimorphism exists. This example is discussed further in Brown and Thomson (2018).

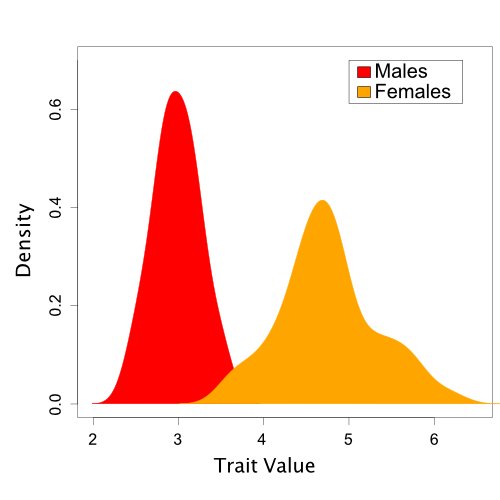
A Single-Normal Model

To start analyzing our data, we fit a single Normal distribution to our trait values using MCMC. This is a reasonable starting point, because we know that many continuous traits are polygenic and normally distributed. This single-normal model includes two free parameters that we estimate from the observed data: the mean and standard deviation.

For the sake of brevity, we will not discuss here how to fit a model using MCMC, but if you are interested the trait values can be found in data.txt, the MCMC analysis can be found in MCMC_SingleNormal.rev, and the results of this analysis (i.e., posterior samples of the mean and standard deviation) can be found in singleNormal_posterior.log. Figure 2 shows some of the parameter values sampled for the mean and standard deviation during the MCMC analysis.

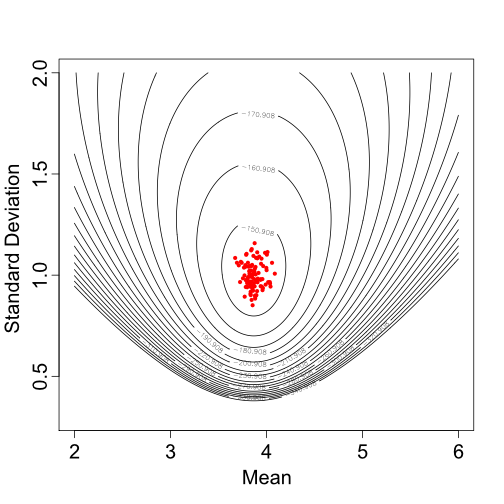
Based on one set of sampled parameter values (one of the dots in Figure 2), Figure 3 shows the resulting Normal distribution compared to the population trait data:

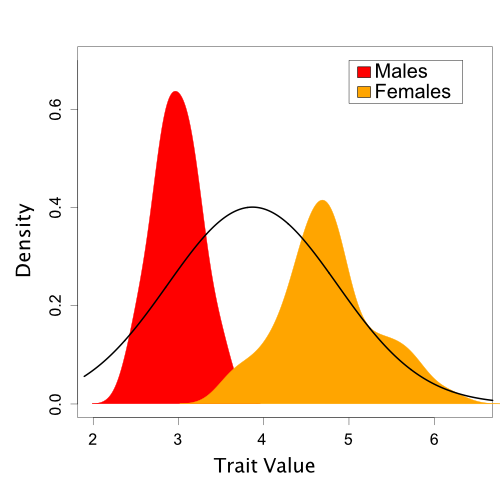
In this case, it is visually obvious that there are some important differences between the model we’ve assumed and the trait data. However, we’d like a quantitative method to assess this fit. Also, in the case of more complicated models and data like we typically encounter in phylogenetics, visual comparisons are often not possible.

Posterior Predictive Simulation

Now that we’ve fit our single-normal model, we need to simulate posterior predictive datasets. Remember that these are datasets of the same size as our observed data, but simulated using means and standard deviations drawn from our posterior distribution.

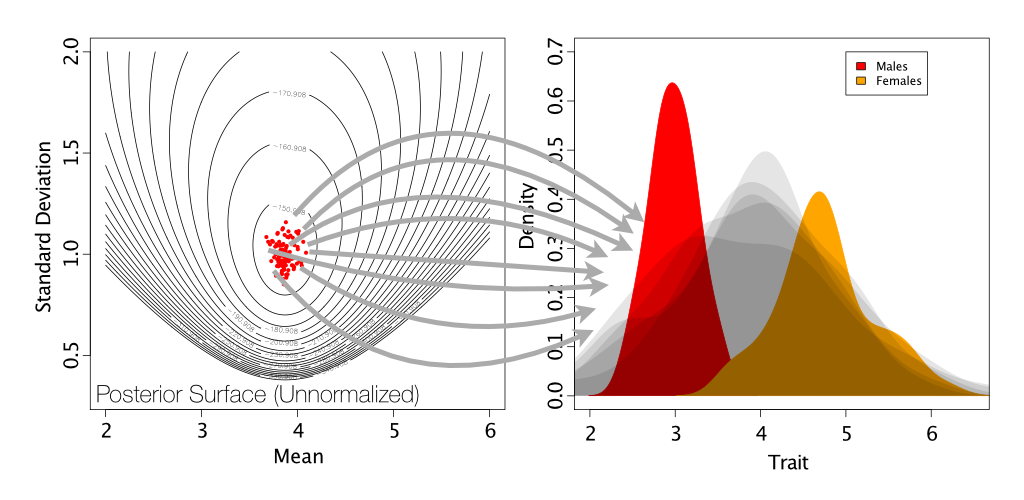
The code for this simulation with the single-normal model can be found in pps_SingleNormal.rev.

# Read in model log file from MCMC
print("Reading MCMC log...")
postVals <- readMatrix("../data/singleNormal_posterior.log")

# Read in empirical data
print("Reading empirical data...")
empDataMatrix <- readMatrix("../data/data.txt")

# Convert empirical data format to a vector
for (i in 1:empDataMatrix.size()){
	empData[i] <- empDataMatrix[i][1] 
}

# Simulate datasets and store in a vector
# Note: We are using the first 49 values as burn-in and we start simulating with the
#       50th value sampled during our MCMC analysis.
print("Posterior predictive simulations...")
for (gen in 50:postVals.size()){
	sims[gen-49] <- rnorm(n=empData.size(), mean=postVals[gen][5], sd=postVals[gen][6])
}

Test Statistics

To quantitatively compare our empirical and simulated data, we need to use some test statistic (or suite of test statistics). These statistics numerically summarize different aspects of a dataset. We can then compare the empirical test statistic value to the posterior predictive distribution. For the case of our trait data, we will try four possible test statistics: the 1st percentile, mean, median, and 90th percentile.

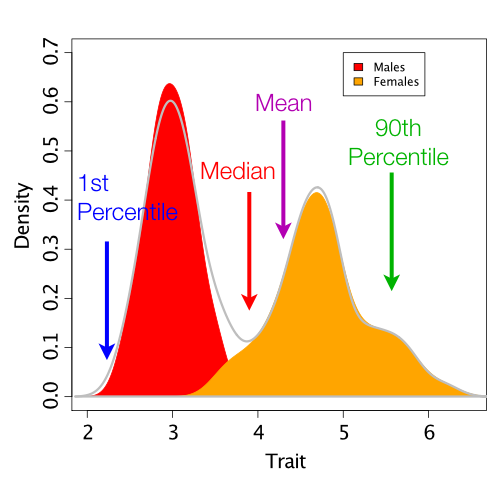
Code to calculate these test statistics can also be found in pps_SingleNormal.rev.

print("Sorting...")

# Sort each simulated dataset
for ( s in 1:sims.size() ){
	sims[s] <- sort(sims[s])
}

# Sort empirical dataset
empData <- sort(empData)

# Define generic function to calculate a chosen percentile, p
function percentile(p,nums){
	pos <- round( (p/100) * nums.size() )
	return nums[pos]
}

print("Calculating test statistics...")

# Calculate empirical test statistics
emp_mean <- mean(empData)
emp_median <- median(empData)
emp_1st <- percentile(1,empData)
emp_90th <- percentile(90,empData)

# Calculate simulated data test statistics
for ( s in 1:sims.size() ){
	sim_means[s] <- mean(sims[s])
	sim_medians[s] <- median(sims[s])
	sim_1sts[s] <- percentile(1,sims[s])
	sim_90ths[s] <- percentile(90,sims[s])
}

Note that the calculation of percentiles is not built-in to RevBayes, which was why we created this custom function

function percentile(p,nums){
	pos <- round( (p/100) * nums.size() )
	return nums[pos]
}

P-values and Effect Sizes

We typically summarize the comparison of test statistic values between empirical and posterior predictive datasets using either a posterior predictive p-value or an effect size.

A posterior predictive p-value tells us how many of our simulated datasets have test statistic values that are as, or more, extreme than the empirical. While useful, these p-values are unable to distinguish between cases where the observed test statisic falls just a little bit outside the posterior predictive distribution from cases where there is a very big difference between the simulated and empirical values.

Effect sizes allow us to distinguish those different possibilities (Doyle et al. 2015). An effect size is calculated as the difference between the empirical test statistic value and the median of the posterior predictive distribution, divided by the standard deviation of the posterior predictive distribution. In other words, how many standard deviations away from the median is the observed value?

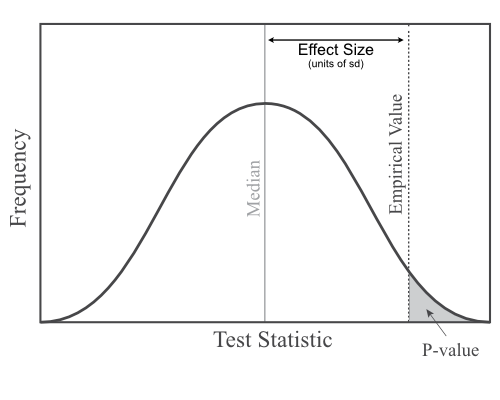
P-values and effect sizes are calculated in pps_SingleNormal.rev with this code

function pVal(e,s){
	greaterThan <- 0
	for (i in 1:s.size()){
		if (e < s[i]){
			greaterThan <- greaterThan + 1
		}
	}
	return greaterThan/s.size()
}

print("Calculating p-values and effect sizes...")

# Calculate posterior predictive p-values
p_means <- pVal(emp_mean,sim_means)
p_medians <- pVal(emp_median,sim_medians)
p_1sts <- pVal(emp_1st,sim_1sts)
p_90ths <- pVal(emp_90th,sim_90ths)

print("")
print("---> Posterior Prediction Model Assessment Results <---")
print("")

# Print p-values
print("P-value mean:",p_means)
print("P-value median:",p_medians)
print("P-value 1st percentile:",p_1sts)
print("P-value 90th percentile:",p_90ths)

# Calculate effect sizes for test statistics
eff_means <- abs(emp_mean-median(sim_means))/stdev(sim_means)
eff_medians <- abs(emp_median-median(sim_medians))/stdev(sim_medians)
eff_1sts <- abs(emp_1st-median(sim_1sts))/stdev(sim_1sts)
eff_90ths <- abs(emp_90th-median(sim_90ths))/stdev(sim_90ths)

# Print effect sizes
print("")
print("Effect size mean:",eff_means)
print("Effect size median:",eff_medians)
print("Effect size 1st percentile:",eff_1sts)
print("Effect size 90th percentile:",eff_90ths)
print("")

The results should look something like this

---> Posterior Prediction Model Assessment Results <---

P-value mean:	0.4973767
P-value median:	0.9632739
P-value 1st percentile:	0.003147954
P-value 90th percentile:	0.3231899

Effect size mean:	0.001805498
Effect size median:	1.860846
Effect size 1st percentile:	2.034433
Effect size 90th percentile:	0.4808086

Note that this script only calculates p-values as the percentage of posterior predictive values that are less than the empirical value. Formally, this is known as a lower one-tailed p-value. Therefore, p-values near either 0 or 1 indicate poor fit between our model and our empirical data.

To run this entire posterior predictive analysis at once, you could use this command from inside the scripts folder for this tutorial.

source(pps_SingleNormal.rev)

These results can also be summarized graphically (although not in RevBayes) like this

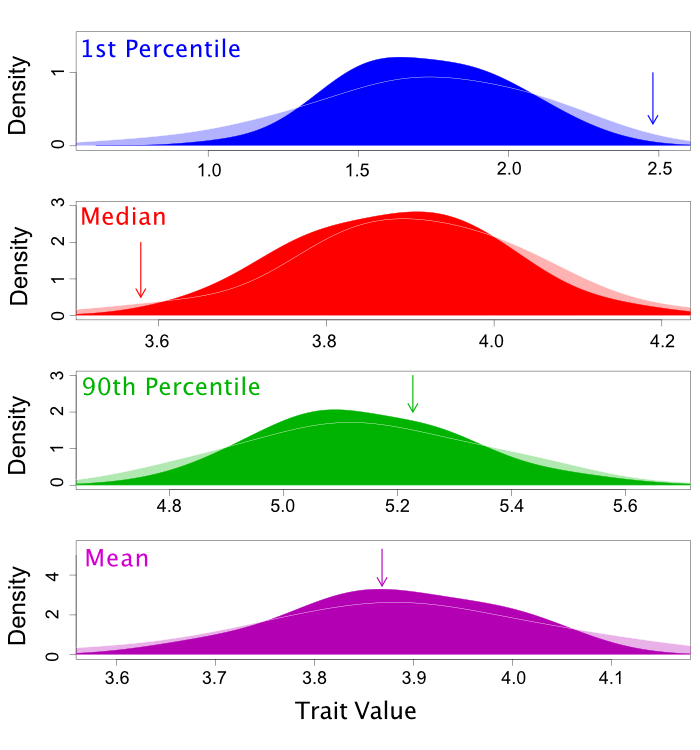
A Two-Normal Model

All of the analyses above can be replicated using a model that correctly employs two independent Normal distributions to separately capture the distinct trait values for males and females. The simplest form of a two-normal model is a mixture distribution. The means and standard deviations of two Normal distributions are estimated separately and we calculate a likelihood that averages across the possibility of each individual belonging to each possible group.

If you want to run an MCMC analysis under this two-normal mixture model, you can use the script MCMC_TwoNormals.rev. However, the MCMC output from this analysis is already available in twoNormals_posterior.log, so you do not need to rerun the MCMC if you don’t want to. You can perform just the posterior prediction steps using pps_TwoNormals.rev.

After running posterior prediction for the two-normal model, compare your results to the one-normal model. Do these results indicate a better fit?

Interpreting Posterior Predictive Results

In general, test statistics with intermediate p-values (close to 0.5) indicate good fit and should have relatively small effect sizes. In our results from the one-normal model, both the mean (p-value = 0.49, effect size = 0.03) and the 90th percentile (p-value = 0.68, effect size = 0.51) do not indicate big discrepancies between what we’ve observed and what we’ve simulated.

However, the median (p-value = 0.046, effect size = 1.70) and 1st percentile (p-value = 0.996, effect size = 1.93) statistics have small and large p-values, respectively, and correspondingly large effect sizes. These results do indicate a discrepancy between the assumptions of the model and the data we’ve observed.

Should we be concerned about our model? Two of our test statistics do not indicate poor fit, while two others do indicate poor fit.

The answer depends on what we want to learn about our population. If we are interested in inferring or predicting the average trait value of our population, we seem to be doing fine. However, if we wanted to predict the trait value of any given individual drawn from the population, we will tend to overpredict individuals with intermediate values and underpredict individuals with extreme trait values. If we were interested in understanding an evolutionary process like stabilizing selection, we might also be very concerned. A single-normal model would suggest that our population has quite a lot of trait variation between individuals, when in fact most of that difference is between sexes. Individuals within a sex have much more limited variation.

Moving to Phylogenetic Posterior Prediction (P³)

After going through this tutorial, you have hopefully gained a sense for the overall workflow of posterior prediction:

1. Fit a model (with MCMC)
2. Simulate posterior predictive datasets by drawing parameter values from the posterior
3. Compare simulated and empirical datasets using your chosen test statistics

A few important, general take-home points are:

• Posterior prediction is a way to assess the absolute fit of a model to your data.
• There is no single correct test statistic to use for posterior prediction.
  • Some statistics may be more sensitive than others to different kinds of model violations.
• How to best proceed if you identify model violations will depend on the goals of your analysis.
  • Is the type of model violation you’ve identified relevant to the question you’re asking?
  • Is the model a better fit for some parts of your dataset than others?
  • Can you think of ways to extend your model that might provide a better fit to your data?

The scripts used for this introductory tutorial made the posterior predictive workflow as obvious as possible, but required us to code each step individually. Because some of these steps are more complicated or tedious for phylogenetic applications, the developers of RevBayes have packaged them in a pipeline called P³ (for Phylogenetic Posterior Prediction). The following tutorials will guide you through the use of P³. These tutorials are divided by the types of test statistics used - whether based solely on the data (data-based) or whether conditioned on the assumed model (inference-based):

Assessing Phylogenetic Reliability Using RevBayes and P³ (Data Version)

Assessing Phylogenetic Reliability Using RevBayes and P³ (Inference Version)

Phyloseminar

A recent phyloseminar discusses the example used in this tutorial and other aspects of posterior prediction:

The Role of Model Fit in Resolving the Tree of Life

1. Bollback J.P. 2002. Bayesian model adequacy and choice in phylogenetics. Molecular Biology and Evolution. 19:1171–1180. 10.1093/oxfordjournals.molbev.a004175
2. Brown J.M. 2014. Predictive approaches to assessing the fit of evolutionary models. Systematic Biology. 63:289–292. 10.1093/sysbio/syu009
3. Brown J.M. 2014. Detection of implausible phylogenetic inferences using posterior predictive assessment of model fit. Systematic Biology. 63:334–348. 10.1093/sysbio/syu002
4. Brown J.M., Thomson R.C. 2018. Evaluating model performance in evolutionary biology. Annual Review of Ecology, Evolution, and Systematics. 49:95–114. 10.1146/annurev-ecolsys-110617-062249
5. Doyle V.P., Young R.E., Naylor G.J.P., Brown J.M. 2015. Can we identify genes with increased phylogenetic reliability? Systematic Biology. 64:824–837. 10.1093/sysbio/syv041
6. Höhna S., Coghill L.M., Mount G.G., Thomson R.C., Brown J.M. 2018. P^3: Phylogenetic Posterior Prediction in RevBayes. Molecular Biology and Evolution. 35:1028–1034. 10.1093/molbev/msx286